Adición de Vectores y su gráfica

La suma de vectores consiste en gráficas, la cual al trazar unas paralela forman la suma de dos vectores, y este es llamado (paralelogramo).

Gráfica de la suma de un vector:

Para sumar los vectores se utiliza dos vectores los cuales son:

Con la suma de estos 2 vectores se refleja el otro origen del vector. mediante rectas paralelas se obtiene un paralelogramo.

Representación Geométrica de un vector suma o resta e nun sistema de coordenadas en R3

Sustracción de Vectores y su gráfica

Restar dos vectores es sumar al primero el opuesto del segundo: u – v = u + (-v)

Gráficamente, u - v es equivalente al segmento orientado cuyo origen es el extremo de v y su extremo es el extremo de u Se aprecia que v + (u-v) = u

Dirección y sentido de un vector en R3

Dirección:

La dirección de un vector está definida por la medida de los ángulos que forma la línea de acción del segmento de recta con los ejes X, Y y Z.

Sentido:

Es la punta de la flecha 

Los Vectores en r3

Significado de r3:

     Esto significa, punto en el espacio tridimensional, es decir que está en 3 dimensiones (ancho largo y alto) por lo tanto se puede representar en un sistema X,Y,Z.

Significado de Vector:

     Es un elemento de un espacio vectorial. Esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo y la dirección. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo.

Vectores en R3:

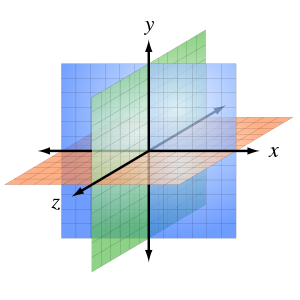
Un sistema de coordenadas tridimensional se construye trazando un eje Z, perpendicular en el origen de coordenadas a los ejes X e Y.

Cada punto viene determinado por tres coordenadas P(x, y, z).

Elementos de un vector en R3:

Módulo de un vector

Un vector no solo nos da una dirección y un sentido, sino también una magnitud, a esa magnitud se le denomina módulo.

Gráficamente: es la distancia que existe entre su origen y su extremo, y se representa por:

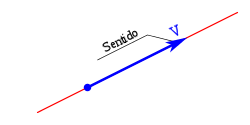
Sentido de un vector

El sentido del vector AB es el que va desde el origen A al extremo B.

Dirección de un vector

La dirección del vector es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.

Gráfica en R3

     Utilizando 3 números reales, se representan éstos como puntos en el espacio, y tres líneas dirigidas a 0 que son perpendiculares entre sí, llamados ejes coordenados y marcados como eje Y, eje Y eje Z.

Las Octantes 

Los ejes de coordenadas determinan tres planos coordenados: XY, XZ e YZ. Estos planos coordenados dividen al espacio en ocho regiones llamadas octantes, en el primer octante las tres coordenadas x, y, z son positivas.

Usos de los Vectores en R3 en la vida diaria

Existen muchos diversos usos de los vectores en R3 en la vida diaria, entre ellos están:

• Arquitectura
• Ingeniería
• Diseño Gráfico
• Ciencias
• Astronomía

Conclusión:

En conclusión se puede decir que R3 significa tridimensional, que un vector es un segmento de recta que tiene un punto de inicio y de fin, ademas de que un vector en R3 es un punto en el espacio tridimensional determinado por un nuevo eje, que sería el Z, que los elementos que hacen que un vector sea correcto son el módulo, sentido y dirección, cabe destacar que para realizar una gráfica de un vector se requieren tres números reales, que son absolutamente todos los números que existen, y se debe tomar en cuenta la cantidad de octantes del plano en este tipo de vector, y por ultimo se debe saber al menos unas pocas aplicaciones de los vectores en R3 en la vida diaria, ya que muy poca gente reconoce que ellos siempre han estado muy presentes en nuestra vida diaria